พีชคณิตของเมตริกซ์ (Algebra of Matrix)

การกระทำระหว่างเมตริกซ์ทางพีชคณิต จะแตกต่างจากจำนวนเลข ตรงที่เมตริกซ์ไม่มีการหารระหว่างเมตริกซ์กับเมตริกซ์ ดังนั้นจะกล่าวถึงการบวกและลบกันของเมตริกซ์ การคูณเมตริกซ์ด้วยปริมาณสเกลาร์ (ที่เป็นจำนวนจริง) และการคูณเมตริกซ์ด้วยเมตริกซ์

การบวกเมตริกซ์ (Matrix Addition)

นิยาม 1 เมตริกซ์ A = [ a_ij] และ B = [ b_ij] จะบวก (หรือลบ) กันได้ก็ต่อเมื่อเมตริกซ์ทั้งสองมีมิติเดียวกัน โดยการนำสมาชิกที่อยู่ในตำแหน่งเดียวกันมาบวกกัน (หรือลบกัน)
คือ [A]_mxn+ [B]_mxn = [ a_ij+ b_ij ]_mxn

ตัวอย่าง 1

$A space equals space open square brackets table row cell negative 2 end cell 1 3 row 0 4 cell negative 6 end cell end table close square brackets comma space B equals space open square brackets table row 1 5 cell negative 3 end cell row 4 2 7 end table close square brackets comma space C equals space open square brackets table row 1 2 row 3 0 end table close square brackets A plus B space equals space open square brackets table row cell open parentheses negative 2 plus 1 close parentheses end cell cell open parentheses 1 plus 5 close parentheses end cell cell open parentheses 3 minus 3 close parentheses end cell row cell open parentheses 0 plus 4 close parentheses end cell cell open parentheses 4 plus 2 close parentheses end cell cell open parentheses negative 6 plus 7 close parentheses end cell end table close square brackets space space space space space space space space space space space space equals space open square brackets table row cell negative 1 end cell 6 0 row 4 6 1 end table close square brackets A minus B space equals space open square brackets table row cell open parentheses negative 2 minus 1 close parentheses end cell cell open parentheses 1 minus 5 close parentheses end cell cell open parentheses 3 plus 3 close parentheses end cell row cell open parentheses 0 minus 4 close parentheses end cell cell open parentheses 4 minus 2 close parentheses end cell cell open parentheses negative 6 minus 7 close parentheses end cell end table close square brackets space space space space space space space space space space space equals space open square brackets table row cell negative 3 end cell cell negative 4 end cell 6 row cell negative 4 end cell 2 cell negative 13 end cell end table close square brackets$

A + C ไม่สามารถหาได้ เพราะ มิติไม่เท่ากัน

การคูณเมตริกซ์ด้วยปริมาณสเกลาร์ (Scaler Multiple of a Matrix)

นิยาม 2 การคูณเมตริกซ์ A = [a_{i j}]_mxn ด้วยปริมาณสเกลาร์ k กระทำได้โดยคูณปริมาณสเกลาร์ k กับทุก ๆ สมาชิกของเมตริกซ์ A คือ

kA = [ k a_{i j} ]_mxn

ตัวอย่าง 2

$A space equals space open square brackets table row 1 2 cell negative 6 end cell row 5 4 7 end table close square brackets minus 3 A space equals space open square brackets table row cell open parentheses negative 3 close parentheses open parentheses 1 close parentheses end cell cell open parentheses negative 3 close parentheses open parentheses 2 close parentheses end cell cell open parentheses negative 3 close parentheses open parentheses negative 6 close parentheses end cell row cell open parentheses negative 3 close parentheses open parentheses 5 close parentheses end cell cell open parentheses negative 3 close parentheses open parentheses 4 close parentheses end cell cell open parentheses negative 3 close parentheses open parentheses 7 close parentheses end cell end table close square brackets space space space space space space space space space equals space open square brackets table row cell negative 3 end cell cell negative 6 end cell 18 row cell negative 15 end cell cell negative 12 end cell cell negative 21 end cell end table close square brackets$

ทฤษฎีบท 1 คุณสมบัติการบวกเมตริกซ์ และการคูณเมตริกซ์ด้วยประมาณสเกลาร์

ให้ A, B, C และ 0 เป็นเมตริกซ์ขนาด mxn และ k_1,k₂ เป็นปริมาณสเกลาร์แล้ว
(1) A + 0 = 0 + A = A (เอกลักษณ์การบวก)
(2) A + (B+C) = (A+B) + C (กฎการจัดหมู่ของการบวก)
(3) (k₁ k₂) A = k₁(k₂A) (กฎการจัดหมู่)
(4) A + B = B + A (กฎการสลับที่ของการบวก)
(5) k₁(A+B) = k₁A + k₁B (กฎการกระจาย)
(6) (k₁+k₂) A = k₁A + k₂A (กฎการกระจาย)
(7) (A^T)^T = A
(8) (A+B)^T = A^T+B^T(9) (kA)^T = k A^T(10) A + (-A) = (-A) + A = 0
(11) ถ้า A+B = A+C แล้ว B = C
(12) k₁(AB) = (k₁A)B = A(k₁B)
สังเกต (A+B+C)^T = A^T+ B^T+ C^T

การคูณเมตริกซ์ด้วยเมตริกซ์ (Matrix Multiplication)

นิยาม 3 ถ้า A เป็นเมตริกซ์ขนาด mxp และ B เป็นเมตริกซ์ขนาด pxn ผลคูณของ A และ B คือ C =A.B จะหาได้ก็ต่อเมื่อจำนวนหลักของเมตริกซ์ A เท่ากับ จำนวนแถวของเมตริกซ์ B ซึ่งผลคูณจะมีจำนวนแถวเท่ากับเมตริกซ์ A และหลักเท่ากับเมตริกซ์

B คือ A_mxp B_p_xn = C_mxn ซึ่งสมาชิกของ C = [c_ij]_mxn คือ c_ij = $sum from k equals 1 to p of a subscript i k end subscript b subscript k j end subscript$
เช่น สมาชิกตำแหน่ง c₁₁ = a₁₁b₁₁ + a₁₂b₂₁ + … +a_1kb_k1

แผนผังของ Falk ช่วยในการหาผลคูณของ C = A.B โดยการเขียนเมตริกซ์ A ทางมุมซ้ายล่าง และ Bทางมุมขวาบนของเมตริกซ์ C สมาชิกของ C อันเกิดจาก A.B จะอยู่ตรงกับแถวที่ i ของ A กับสดมภ์ที่ k ของ B ดังแผนผัง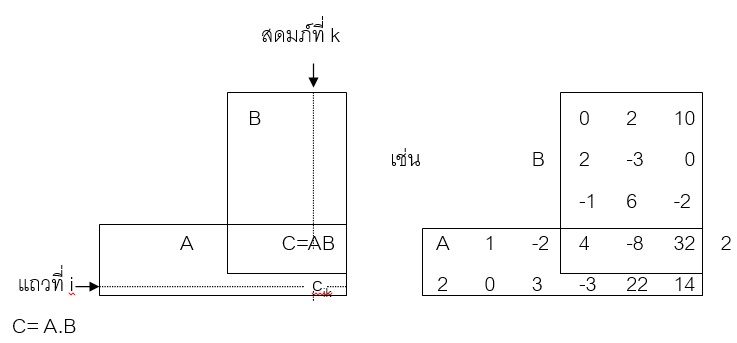

ตัวอย่าง 3 จงหาผลคูณของเมตริกซ์
$A space equals open square brackets table row 2 cell negative 2 end cell 0 row 3 1 4 end table close square brackets$ กับ $n space equals open square brackets table row 1 3 cell negative 1 end cell row 2 cell negative 2 end cell 0 row 1 0 4 end table close square brackets$

วิธีทำ

1
3
-1

2
-2
0

1
0
4
2
-2
0
-2
10
-2
3
1
4
9
7
13

คือ
$A times B space equals open square brackets table row cell negative 2 end cell 10 cell negative 2 end cell row 9 7 13 end table close square brackets$

ตัวอย่าง 4
ถ้า $A squared equals open square brackets table row 4 8 cell negative 8 end cell row 0 4 cell negative 8 end cell row 0 0 4 end table close square brackets$ จงหา A

ข้อสังเกต
          เมตริกซ์ที่สมาชิกใต้เส้นทแยงมุมเป็นศูนย์ เมื่อคูณกับตัวเองกี่ครั้งก็ตาม สมาชิกใต้เส้นทแยงมุมจะเป็นศูนย์เหมือนเดิม และสมาชิกในแนวทแยงมุมจะเท่ากับค่าของมันยกกำลังเท่ากับครั้งที่คูณ เช่น
$A equals open square brackets table row 1 2 3 row 0 4 2 row 0 0 3 end table close square brackets space space space A squared equals open square brackets table row 1 10 16 row 0 16 14 row 0 0 9 end table close square brackets$

วิธีทำ ให้
$A space equals space open square brackets table row 2 a b row 0 2 c row 0 0 2 end table close square brackets A squared space equals space open square brackets table row 4 cell 4 a end cell cell 2 b plus a c plus 2 b end cell row 0 4 cell 2 c plus 2 c end cell row 0 0 4 end table close square brackets space equals space open square brackets table row 4 8 cell negative 8 end cell row 0 4 cell negative 8 end cell row 0 0 4 end table close square brackets$

ได้ 4a = 8    a = 2
4c = -8         c = -2
4b = -4         b = -1

ดังนั้น $A space equals space open square brackets table row 2 2 cell negative 1 end cell row 0 2 cell negative 2 end cell row 0 0 2 end table close square brackets$

ข้อสังเกต

ถ้า AB และ BA หาค่าได้ ไม่จำเป็นที่ AB = BA

ตัวอย่าง 5

$open square brackets table row 1 0 row cell negative 2 end cell 4 end table close square brackets open square brackets table row cell negative 2 end cell 6 row 1 3 end table close square brackets equals open square brackets table row cell negative 2 end cell 6 row 8 0 end table close square brackets$
แต่ $open square brackets table row cell negative 2 end cell 6 row 1 3 end table close square brackets open square brackets table row 1 0 row cell negative 2 end cell 4 end table close square brackets equals open square brackets table row cell negative 14 end cell 24 row cell negative 5 end cell 12 end table close square brackets$

2. ถ้า AB = AC ไม่สามารถสรุปได้ว่า B = C

ตัวอย่าง 6

$open square brackets table row 1 1 row 3 3 end table close square brackets open square brackets table row 4 2 row 3 16 end table close square brackets equals open square brackets table row 1 1 row 3 3 end table close square brackets open square brackets table row 2 7 row 5 11 end table close square brackets space space space space space space space space space space space space space space space space space space space space space space space space equals open square brackets table row 7 18 row 21 54 end table close square brackets$
แต่
   $open square brackets table row 4 2 row 3 16 end table close square brackets not equal to open square brackets table row 2 7 row 5 11 end table close square brackets$

3. ถ้า AB = [0] ทั้ง A และ B ไม่จำเป็นต้องเป็น เมตริกซ์ศูนย์

ตัวอย่าง 7

$open square brackets table row 1 2 row 0 0 end table close square brackets open square brackets table row 6 4 row cell negative 3 end cell cell negative 2 end cell end table close square brackets equals open square brackets table row 0 0 row 0 0 end table close square brackets$

ทฤษฎีบท 2 คุณสมบัติของ การคูณเมตริกซ์ด้วยเมตริกซ์

ให้ A,B และ C เป็นเมตริกซ์ที่คูณกันได้แล้ว
1.) A(BC) = (AB)C (กฎการจัดหมู่)
2) A(B+C)    = AB + AC (กฎการกระจาย)
3) (A+B)C    = AC + BC (กฎการกระจาย)
4) (AB)^T = B^TA^T
5) AI = IA = A (เอกลักษณ์การคูณ)
สังเกต (ABC)^T = C^TB^TA^T

ตัวอย่าง 8 จงหาผลคูณของเมตริกซ์ที่กำหนดให้ต่อไปนี้
(ก) $A equals open square brackets table row 4 7 row 3 5 end table close square brackets comma space space space B equals open square brackets table row 9 cell negative 2 end cell row 6 8 end table close square brackets$
(ข) $A equals open square brackets table row 5 8 row 1 0 row 2 7 end table close square brackets comma space space space B equals open square brackets table row cell negative 4 end cell cell negative 3 end cell row 2 0 end table close square brackets$

วิธีทำ
(ก) $A B space equals space open square brackets table row cell open parentheses 4 close parentheses open parentheses 9 close parentheses plus end cell cell open parentheses 7 close parentheses open parentheses 6 close parentheses end cell cell open parentheses 4 close parentheses open parentheses negative 2 close parentheses plus end cell cell open parentheses 7 close parentheses open parentheses 8 close parentheses end cell row cell open parentheses 3 close parentheses open parentheses 9 close parentheses plus end cell cell open parentheses 5 close parentheses open parentheses 6 close parentheses end cell cell open parentheses 3 close parentheses open parentheses negative 2 close parentheses plus end cell cell open parentheses 5 close parentheses open parentheses 8 close parentheses end cell end table close square brackets space space space space space space equals open square brackets table row 78 48 row 57 34 end table close square brackets$
(ข) $A B space equals open square brackets table row cell open parentheses 5 close parentheses open parentheses negative 4 close parentheses plus end cell cell open parentheses 8 close parentheses open parentheses 2 close parentheses end cell cell open parentheses 5 close parentheses open parentheses negative 3 close parentheses plus end cell cell open parentheses 8 close parentheses open parentheses 0 close parentheses end cell row cell open parentheses 2 close parentheses open parentheses negative 4 close parentheses plus end cell cell open parentheses 7 close parentheses open parentheses 2 close parentheses end cell cell open parentheses 2 close parentheses open parentheses negative 3 close parentheses plus end cell cell open parentheses 7 close parentheses open parentheses 0 close parentheses end cell end table close square brackets space space space space space space equals space open square brackets table row cell negative 4 end cell cell negative 15 end cell row cell negative 4 end cell cell negative 3 end cell row 6 cell negative 6 end cell end table close square brackets$

การคูณเมตริกซ์ด้วยเมตริกซ์ไม่เป็นไปตามกฎการสลับที่ นั่นคือ BA ¹ AB สังเกตได้จาก ตัวอย่าง 9 (ก) ส่วนตัวอย่าง 9(ข) BA หาไม่ได้ เนื่องจากเมตริกซ์ตัวตั้งมีจำนวนหลักไม่เท่ากับจำนวนแถวของเมตริกซ์ตัวคูณ

ตัวอย่าง 10 จงหาผลคูณของเมตริกซ์ที่กำหนดให้ต่อไปนี้
(ก) $A space equals open square brackets table row 2 cell negative 1 end cell 3 row 0 4 5 row 1 cell negative 7 end cell 9 end table close square brackets space space space B equals open square brackets table row cell negative 3 end cell row 6 row 4 end table close square brackets$
(ข) $A equals space open square brackets table row cell negative 4 end cell 2 row 3 8 end table close square brackets space space space B equals open square brackets table row cell X subscript 1 end cell row cell X subscript 2 end cell end table close square brackets$

วิธีทำ
(ก)
$A B space equals space open square brackets table row 2 cell negative 1 end cell 3 row 0 4 5 row 1 cell negative 7 end cell 9 end table close square brackets open square brackets table row cell negative 3 end cell row 6 row 4 end table close square brackets space space space space space space space equals open square brackets table row cell open parentheses 2 close parentheses open parentheses negative 3 close parentheses plus end cell cell open parentheses negative 1 close parentheses open parentheses 6 close parentheses plus end cell cell open parentheses 3 close parentheses open parentheses 4 close parentheses end cell row cell open parentheses 0 close parentheses open parentheses negative 3 close parentheses plus end cell cell open parentheses 4 close parentheses open parentheses 6 close parentheses plus end cell cell open parentheses 5 close parentheses open parentheses 4 close parentheses end cell row cell open parentheses 1 close parentheses open parentheses negative 3 close parentheses plus end cell cell open parentheses negative 7 close parentheses open parentheses 6 close parentheses plus end cell cell open parentheses 9 close parentheses open parentheses 4 close parentheses end cell end table close square brackets space space space space space space space equals space open square brackets table row 0 row 44 row cell negative 9 end cell end table close square brackets$
(ข)
$A B space equals open square brackets table row cell negative 4 end cell 2 row 3 8 end table close square brackets open square brackets table row cell X subscript 1 end cell row cell X subscript 2 end cell end table close square brackets space space space space space equals space open square brackets table row cell negative 4 x subscript 1 plus end cell cell 2 x subscript 2 end cell row cell 3 x subscript 1 plus end cell cell 8 x subscript 2 end cell end table close square brackets$

ตัวอย่างที่ 11
(ก) $open square brackets table row 2 1 row 1 0 row cell negative 1 end cell 2 end table close square brackets open square brackets table row 1 cell negative 1 end cell 3 0 row 2 1 2 2 end table close square brackets space equals space open square brackets table row 4 cell negative 1 end cell 8 2 row 1 cell negative 1 end cell 3 0 row 3 3 1 4 end table close square brackets$
(ข) $open square brackets table row 1 cell negative 1 end cell 3 0 row 2 1 2 2 end table close square brackets open square brackets table row 2 1 row 1 0 row cell negative 1 end cell 2 end table close square brackets$

หาไม่ได้ เนื่องจากเมตริกซ์ตัวตั้งมีจำนวนหลักไม่เท่ากับจำนวนแถวของเมตริกซ์ตัวคูณ

(ค)     $open square brackets table row 2 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets open square brackets table row 1 2 row 1 2 end table close square brackets space equals space open square brackets table row 4 8 row cell negative 2 end cell cell negative 4 end cell end table close square brackets$
(ง)      $open square brackets table row 1 2 row 1 2 end table close square brackets open square brackets table row 2 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets space equals space open square brackets table row 0 0 row 0 0 end table close square brackets$
(จ)      $open square brackets table row 2 cell negative 3 end cell 0 end table close square brackets open square brackets table row cell negative 5 end cell row 2 row cell negative 2 end cell end table close square brackets space equals space open square brackets table row cell negative 16 end cell end table close square brackets$
(ฉ)      $open square brackets table row cell negative 5 end cell row 2 row cell negative 2 end cell end table close square brackets open square brackets table row 2 cell negative 3 end cell 0 end table close square brackets space equals space open square brackets table row cell negative 10 end cell 15 0 row 4 cell negative 6 end cell 0 row cell negative 4 end cell 6 0 end table close square brackets$

ตัวอย่าง 12 ถ้า $A space equals open square brackets table row 2 1 row 0 2 end table close square brackets$ แล้ว ให้หา A¹⁰⁰

วิธีทำ
$A space equals open square brackets table row 2 1 row 0 2 end table close square brackets A squared space equals space open square brackets table row 2 1 row 0 2 end table close square brackets open square brackets table row 2 1 row 0 2 end table close square brackets space equals space open square brackets table row cell 2 squared end cell cell 2 plus 2 end cell row 0 cell 2 squared end cell end table close square brackets A to the power of 3 space end exponent equals space open square brackets table row 2 1 row 0 2 end table close square brackets open square brackets table row cell 2 squared end cell cell 2 plus 2 end cell row 0 cell 2 squared end cell end table close square brackets space space space space equals open square brackets table row cell 2 cubed end cell cell 2 squared plus end cell cell 2 squared plus end cell cell 2 squared end cell row 0 blank cell 2 cubed end cell blank end table close square brackets space space space space space equals space open square brackets table row cell 2 cubed end cell cell 3 open parentheses 2 squared close parentheses end cell row 0 cell 2 cubed end cell end table close square brackets A to the power of 4 space end exponent equals space open square brackets table row 2 1 row 0 2 end table close square brackets open square brackets table row cell 2 cubed end cell cell 2 squared plus end cell cell 2 squared plus end cell cell 2 squared end cell row 0 blank cell 2 cubed end cell blank end table close square brackets space space space space space equals space open square brackets table row cell 2 to the power of 4 end cell cell 2 cubed plus end cell cell 2 cubed plus end cell cell 2 cubed plus end cell cell 2 cubed end cell row 0 blank blank cell 2 to the power of 4 end cell blank end table close square brackets space space space space space equals open square brackets table row cell 2 to the power of 4 end cell cell 4 open parentheses 2 cubed close parentheses end cell row 0 cell 2 to the power of 4 end cell end table close square brackets therefore space A to the power of 100 space equals space open square brackets table row cell 2 to the power of 100 end cell cell 100 open parentheses 2 to the power of 99 close parentheses end cell row 0 cell 2 to the power of 100 end cell end table close square brackets$

การบวกเมทริกซ์ การคูณเมทริกซ์กับจำนวนจริง การคูณระหว่างเมทริกซ์

แบบฝึกหัด

การบวกเมทริกซ์ การคูณเมทริกซ์กับจำนวนจริง การคูณระหว่างเมทริกซ์

การบวกเมทริกซ์ การคูณเมทริกซ์กับจำนวนจริง การคูณระหว่างเมทริกซ์

การบวกเมทริกซ์ การคูณเมทริกซ์กับจำนวนจริง การคูณระหว่างเมทริกซ์

เนื้อหา

พีชคณิตของเมตริกซ์ (Algebra of Matrix)

การบวกเมตริกซ์ (Matrix Addition)

การคูณเมตริกซ์ด้วยปริมาณสเกลาร์ (Scaler Multiple of a Matrix)

ทฤษฎีบท 1 คุณสมบัติการบวกเมตริกซ์ และการคูณเมตริกซ์ด้วยประมาณสเกลาร์

การคูณเมตริกซ์ด้วยเมตริกซ์ (Matrix Multiplication)

ข้อสังเกต

ทฤษฎีบท 2 คุณสมบัติของ การคูณเมตริกซ์ด้วยเมตริกซ์

ทีมผู้จัดทำ

บทเรียน

ติดต่อเรา

ติดตามเรา

เราในสื่ออื่นๆ